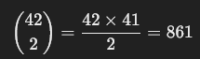Ich gewinne nie etwas

Das Gute daran ist, daß die ganzen unglücklichen Lottospieler die glücklichen Gewinner fördern.
Wenn nichts reinkommt an Geld, würde einem auch ein Sechser nix einbringen.

Deutsches Lotto ist ja auch wie Eurojackpot furchtbar, weil alle auf den Riesenjackpot gieren, während die unteren Kategorien lausig sind. Wenn überhaupt empfehle ich aus statistischer Sicht polnisches Mini Lotto. Der Schein kostet nur 50 Cent, es gibt nur 5 aus 42 Zahlen ohne Zusatzzahlen, bei zwei Richtigen mit der Gewinnwahrscheinlichkeit 1/11 gewinnt man schon einen Euro, und bei vier Richtigen 100 Euro. Der Jackpot beträgt allerdings auch "nur" 100.000 Euro. Aber dann würden sich wenigstens die Verluste in Grenzen halten.
Der mathematische Teil in mir wird den Spaß am Glücksspiel ohnehin nie verstehen.

Aufgrund des äußerst scharfsinnigen und klugen Mitforisten
H3rzwetter
muss ich leider den Mittelteil meines Kommentares streichen.
Was bleibt? Glücksspiel ist doof. 🙂

Selbst-Bewusst77 meinte:

bei zwei Richtigen mit der Gewinnwahrscheinlichkeit 1/11 gewinnt man schon einen Euro

Zum Vergrößern anklicken....

Könntest du mir mal vorrechnen, wie man auf so eine hohe Gewinnwahrscheinlichkeit bei 2 aus 42 kommt?
Ich komme da grob geschätzt auf 1 zu 1600

H3rzwetter meinte:

Könntest du mir mal vorrechnen, wie man auf so eine hohe Gewinnwahrscheinlichkeit bei 2 aus 42 kommt?
Ich komme da grob geschätzt auf 1 zu 1600

Zum Vergrößern anklicken....

Hab ich fairerweise nicht selber durchkalkuliert, sondern der angehängten Tabelle des Betreibers entnommen.
Aber hast Du bei Deiner Berechnung bedacht, dass 5 mal Zahlen gezogen werden, und sich nach jeder Zahl die verbleibende Anzahl der ziehbaren Zahlen verringert?

Die Formel für 5 Richtige müsste doch
42 * 41* 40* 39* 38 * 37
5 * 4 * 3 * 2 * 1
lauten?

Hmm, ich glaube, Du hast recht. Bin nur ein Laie. Entschuldigung.

H3rzwetter meinte:

Könntest du mir mal vorrechnen, wie man auf so eine hohe Gewinnwahrscheinlichkeit bei 2 aus 42 kommt?
Ich komme da grob geschätzt auf 1 zu 1600

Zum Vergrößern anklicken....

Jetzt habe ich doch mal versucht selber zu rechnen.
P(X=k)=(nN)(kK)(n−kN−K)
N = Gesamtanzahl der möglichen Zahlen (hier: 42)
KKK = Anzahl der Gewinnzahlen (hier: 5)
nnn = Anzahl der gezogenen Zahlen (hier: 5)
kkk = Anzahl der gewünschten Treffer (hier: 2)
P(X=2)=850,66810×7770≈0.0913

Komm da auch auf 9,13%, also etwa 1 : 11. Weiss aber nicht, wo der Fehler in meiner Formel ist. 😭

Ich habe es so versucht:
Wahrscheinlichkeit bei 1 aus 42 ist klar: 1/42
Wahrscheinlichkeit bei 2 aus 42 muß logischerweise viel geringer sein, mM nach nimmt man einfach die zwei Fälle und dividiert sie durch die Kombinationen also 42*41 also 2/ca. 1600 = 1/800

H3rzwetter meinte:

Ich habe es so versucht:
Wahrscheinlichkeit bei 1 aus 42 ist klar: 1/42
Wahrscheinlichkeit bei 2 aus 42 muß logischerweise viel geringer sein, mM nach nimmt man einfach die zwei Fälle und dividiert sie durch die Kombinationen also 42*41 also 2/ca. 1600 = 1/800

Zum Vergrößern anklicken....

Hmm, die Annahme, dass man die Wahrscheinlichkeit für "2 aus 42" berechnen kann, indem man einfach die Wahrscheinlichkeit für "1 aus 42" quadriert ist müsste aber eigentlich falsch sein
Das liegt daran, dass die Berechnung der Wahrscheinlichkeit für einen Gewinn in einer Lotterie eine kombinatorische Wahrscheinlichkeit ist und nicht einfach durch das Multiplizieren einzelner Wahrscheinlichkeiten berechnet werden kann. Die Annahme, dass man die Wahrscheinlichkeit für den zweiten Treffer multiplizieren kann, setzt voraus, dass diese beiden Ereignisse unabhängig voneinander sind. In einer Lotterie ist das ja aber nicht der Fall, da die gezogenen Zahlen ohne Zurücklegen gezogen werden. Die Wahrscheinlichkeit für jede nachfolgende Zahl hängt also davon ab, welche Zahlen bereits gezogen wurden.

In einer Lotterie "5 aus 42" spielt die Reihenfolge doch eigentlich keine Rolle? Es wird doch nur nur betrachtet, welche Zahlen richtig sind, unabhängig davon, in welcher Reihenfolge sie gezogen wurden. Bei Deinem Rechenweg würde man die Reihenfolge berücksichtigen, was hier jedoch nicht korrekt wäre.
Der korrekte Ansatz müsste meiner Meinung nach Binomialkoeffizienten verwenden, um die Anzahl der Möglichkeiten zu berechnen, aus der Gesamtmenge N=42N = 42N=42 eine bestimmte Anzahl kkk (hier 2) an Gewinnzahlen auszuwählen und die restlichen Zahlen nicht zu treffen.
Die richtige Methode müsste also die Verwendung der hypergeometrischen Verteilung sein, welche alle möglichen Kombinationen und Verhältnisse zwischen gezogenen und nicht gezogenen Zahlen berücksichtigt.

Gibt es Mathematiker und Mathebegeisterte hier im Forum die uns weiterhelfen können? 😱

Naja, ist doch aber logisch:
Es gibt 42*41 Möglichkeiten für zwei Zahlen an Kombinationen und 2!(Fakultät) Fälle, die richtig sind: Zuerst die 2 und dann die 1 oder umgekehrt.

Würde man 42 aus 42 ziehen, hätte man 42!/42!= 1

H3rzwetter meinte:

Würde man 42 aus 42 ziehen, hätte man 42!/42!= 1

Zum Vergrößern anklicken....

Hmm, Deine Argumentation basiert auf der Berechnung der Permutation (Reihenfolge wichtig) statt der Kombination (Reihenfolge unwichtig).
Bei einer Lotterie geht es darum, eine bestimmte Anzahl von Zahlen zu treffen, unabhängig von der Reihenfolge. Das bedeutet, es müsste mit Kombinationen gerechnet werden.
Eine Permutation berücksichtigt, in welcher Reihenfolge die Zahlen gezogen werden, weshalb es bei 2! (2 Fakultät) verschiedene Anordnungen für zwei Zahlen gibt (zum Beispiel: "1, 2" und "2, 1"). Bei einer Lotterie zählt aber doch eigentlich nur, dass man zwei bestimmte Zahlen getroffen hat, nicht in welcher Reihenfolge sie erschienen sind.
Du gibst an, dass es 42×41 Möglichkeiten gibt, zwei Zahlen aus 42 auszuwählen. Das ist aber doch die Berechnung für Permutationen, nicht für Kombinationen.
Die Formel für die Permutationen von zwei Elementen aus 42 wäre: 42×41=1,72242 Das berücksichtigt die Reihenfolge der gezogenen Zahlen. Bei einer Lotterie interessiert aber doch nur, welche Zahlen gezogen wurden, nicht in welcher Reihenfolge sie erschienen.
Richtiger wäre meine Meinung nach 861. Ich habe dabei die angehängte Formel genutzt.
Du gehst davon aus, dass es 2!=2 "richtige Fälle" gibt. Diese zwei "richtigen Fälle" beziehen sich auf die Reihenfolge der zwei Treffer, also entweder "Treffer 1, Treffer 2" oder "Treffer 2, Treffer 1".
Tatsächlich müsste es jedoch unerheblich sein, ob der Treffer "1" vor dem Treffer "2" kommt.
Somit ist die Anzahl der "richtigen Fälle" tatsächlich 1, und nicht 2!. Es gibt meiner Meinung nach genau eine Möglichkeit, diese zwei richtigen Zahlen zu haben, unabhängig von der Reihenfolge.

Aber sicher bin ich mir fairerweise nicht. 😥